En fechas recientes, un grupo de investigadores de nuestro instituto ha dado a conocer un artículo relativo al desarrollo de pliegues de propagación de falla. En el mismo se debate la aplicación del modelo cinemático de trishear para comprender la cinemática y la geometría de estos pliegues.

Sin embargo, se ha observado que la geometría resultante en casos naturales puede desviarse de las predicciones del modelo trishear dependiendo de las propiedades reológicas involucradas en la deformación. Para abordar esta limitación, los autores implementaron modelos numéricos viscoplásticos por elementos finitos.

 

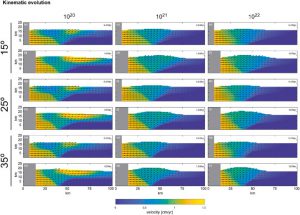
Figura 1. Evolución cinemática de los modelos de elementos finitos con ángulos de falla de 15º, 25º y 35º.

Los resultados obtenidos revelaron que en modelos con un ángulo de falla de 15°, estas simulaciones desarrollan una discontinuidad mecánicamente más débil, que se define como la zona de baja viscosidad (LVZ). La LVZ induce fallas y absorbe el deslizamiento, causando desviaciones en los vectores de velocidad respecto a la alineación paralela con la rampa inversa principal. En modelos con ángulos de falla de 25° o 35°, los vectores cinemáticos de la pared colgante se alinearon paralelamente a la rampa, y se observó una zona de rotación progresiva de los vectores de velocidad en el forelimb, lo que se asemeja a la zona teórica de trishear. En estos escenarios, los pliegues resultantes exhibieron mayor simetría. Sin embargo, en capas de cobertura con una viscosidad igual a 10²⁰ Pa s, el forelimb exhibe las velocidades más altas, lo cual se atribuye al flujo del material hacia la pared de pie.

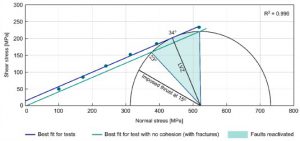
Figura 3. El círculo de Mohr-Coulomb construido a partir de las tensiones principales obtenidas de las pruebas de elementos finitos.

 

La cita completa a este artículo es:

Plotek, B., Likerman, J., & Cristallini, E. (2024). Geomechanical modeling of fault-propagation folds: A comparative analysis of finite-element and the trishear kinematic model. Journal of Structural Geology, 180, 105064.